2. Cross Product

Exercises

a. Determinants

1

2

3

1. Find the determinant of the matrix \(\begin{pmatrix} 5 & 2 \\ 3 & -1 \end{pmatrix}\)

   The determinant is \( \begin{vmatrix} 5 & 2 \\ 3 & -1 \end{vmatrix}=-11\)

   To find the determinant, multiply the principle diagonal entries and subtract the product of the off diagonal entries \[\begin{aligned} \begin{vmatrix} 5 & 2 \\ 3 & -1 \end{vmatrix} =5\cdot(-1)-2\cdot3=-5-6=-11 \end{aligned}\]

   lh 

2. Find the determinant of the matrix \(\begin{pmatrix} 1 & 2 & 3 \\ -5 & 1 & 4 \\ 3 & 2 & 1 \end{pmatrix}\)

   To find the determinant, use the expansion by minors. For example \[\begin{aligned} \begin{vmatrix} a & d & g \\ b & e & h \\ c & f & i \end{vmatrix} =a\begin{vmatrix} e & h \\ f & i \end{vmatrix} -d\begin{vmatrix} b & h \\ c & i \end{vmatrix} +g\begin{vmatrix} b & e \\ c & f \end{vmatrix} \end{aligned}\]

   The determinant is \( \begin{vmatrix} 1 & 2 & 3 \\ -5 & 1 & 4 \\ 3 & 2 & 1 \end{vmatrix}=-12\)

   Using the expansion on the top row: \[\begin{aligned} \begin{vmatrix} 1 & 2 & 3 \\ -5 & 1 & 4 \\ 3 & 2 & 1 \end{vmatrix} &=1(1\cdot1-4\cdot2)-2(-5\cdot1-4\cdot3)+3(-5\cdot2-3\cdot1) \\ &=-7+34-39 =-12 \end{aligned}\]

   lh 

3. Find the determinant \(\begin{vmatrix} 2 & 4 & 1 \\ -3 & 0 & 4 \\ 1 & 3 & 1 \end{vmatrix}\)

   Expansion by minors on the \(2^\text{nd}\) row will be faster because there is a \(0\).

   The determinant is \( \begin{vmatrix} 2 & 4 & 1 \\ -3 & 0 & 4 \\ 1 & 3 & 1 \end{vmatrix}=-5\)

   Using the expansion by minors on the \(2^\text{nd}\) row: \[\begin{aligned} \begin{vmatrix} 2 & 4 & 1 \\ -3 & 0 & 4 \\ 1 & 3 & 1 \end{vmatrix} &=3(4\cdot1-1\cdot3)+0(*)-4(2\cdot3-4\cdot1) \\ &=3-8=-5 \end{aligned}\]

   lh 

4. Find the determinant of the matrix \(\begin{vmatrix} 1 & 3 & 0 & 4 \\ 0 & 2 & 1 & 5 \\ 0 & 3 & 5 & 1 \\ 2 & 0 & 0 & 2 \end{vmatrix}\)

   To find the determinant, use expansion by minors. The best (easiest) way to approach this problem is to expand on the \(1^\text{st}\) column or \(4^\text{th}\) row (since there are two zeros). Remember to use the checkerboard to put the right signs in: \[\begin{pmatrix} + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ + & - & + & - & \cdots \\ - & + & - & + & \cdots \\[4pt] \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix}\]

   The determinant is \( \begin{vmatrix} 1 & 3 & 0 & 4 \\ 0 & 2 & 1 & 5 \\ 0 & 3 & 5 & 1 \\ 2 & 0 & 0 & 2 \end{vmatrix}=102\)

   We expand on the \(4^\text{th}\) row because it has two \(0\)'s. (This is easiest.): \[\begin{aligned} \begin{vmatrix} 1 & 3 & 0 & 4 \\ 0 & 2 & 1 & 5 \\ 0 & 3 & 5 & 1 \\ 2 & 0 & 0 & 2 \end{vmatrix} &=-2 \begin{vmatrix} 3 & 0 & 4 \\ 2 & 1 & 5 \\ 3 & 5 & 1 \end{vmatrix} +0-0+2 \begin{vmatrix} 1 & 3 & 0 \\ 0 & 2 & 1 \\ 0 & 3 & 5 \end{vmatrix} \end{aligned}\] Now we have two \(3\times3\) matrices to compute, the first on the \(1^\text{st}\) row and the second on the \(1^\text{st}\) column:: \[\begin{aligned} \begin{vmatrix} 1 & 3 & 0 & 4 \\ 0 & 2 & 1 & 5 \\ 0 & 3 & 5 & 1 \\ 2 & 0 & 0 & 2 \end{vmatrix} &=\begin{array}{ll} -2\big[3(1\cdot1-5\cdot5)-0+4(2\cdot5-1\cdot3)\big] \\[3pt] +2\big[1(2\cdot5-1\cdot3)-0+0\big] \end{array} \\ &=-2[-3\cdot24+4\cdot7]+2[10-3] \\ &=-2(-44)+2\cdot7 =102 \end{aligned}\]

   lh 

b. Cross Product and Triple Product

1

2

3

4

5

5. Find the cross product \(\vec u\times\vec v\) when \(\vec u=(3,0,2)\) and \(\vec v=(1,2,1)\)

   The cross product is the determinant of the matrix with \(\hat{\imath},\hat{\jmath},\hat{k}\) on the first row, and the vectors \(\vec u\) and \(\vec v\) on the second and third rows: \[\begin{aligned} \vec u\times\vec v =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} \end{aligned}\]

   \(\vec u\times\vec v=\langle -4,-1,6 \rangle\)

   To find the cross product, we build a matrix with \(\hat{\imath},\hat{\jmath},\hat{k}\) on the first row, and the vectors \(\vec u\) and \(\vec v\) on the second and third rows. Then we find the determinant: \[\begin{aligned} \vec u\times\vec v &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 3 & 0 & 2 \\ 1 & 2 & 1 \end{vmatrix} \\ &=\hat\imath(0\cdot1-2\cdot2)-\hat\jmath(3\cdot1-2\cdot1) +\hat k(3\cdot2-0\cdot1) \\ &=\hat\imath(-4)-\hat\jmath(1)+\hat k(6) =\langle-4,-1,6\rangle \end{aligned}\]

   lh 

   Don't forget the extra minus before the \(\hat\jmath\) term.

6. Find the cross product \(\vec a\times\vec b\) when \(\vec a=(-1,2,1)\) and \(\vec b=(3,5,2)\)

   \(\vec a\times\vec b=(-1,5,-11)\)

   To find the cross product, we build a matrix with \(\hat{\imath},\hat{\jmath},\hat{k}\) on the first row, and the vectors \(\vec a\) and \(\vec b\) on the second and third rows. Then we find the determinant: \[\begin{aligned} \vec a\times\vec b &=\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ -1 & 2 & 1 \\ 3 & 5 & 2 \end{vmatrix} \\ &=\hat\imath(2\cdot2-1\cdot5)-\hat\jmath(-1\cdot2-1\cdot3)+\hat k(-1\cdot 5-2\cdot3) \\ &=\hat\imath(-1)-\hat\jmath(-5)+\hat k(-11) =(-1,5,-11) \end{aligned}\]

   lh 

7. Find the cross product \(\vec u\times\vec v\) when \(\vec u=(3,8,2)\) and \(\vec v=(1,5,-5)\)

   \(\vec u\times\vec v=(-50,17,7)\)

   To find the cross product, we build a matrix with \(\hat{\imath},\hat{\jmath},\hat{k}\) on the first row, and the vectors \(\vec u\) and \(\vec v\) on the second and third rows. Then we find the determinant: \[\begin{aligned} \vec u\times\vec v &=\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 3 & 8 & 2 \\ 1 & 5 & -5 \end{vmatrix} \\ &=\hat\imath(8\cdot(-5)-2\cdot5)-\hat\jmath(3\cdot(-5)-2\cdot1) +\hat k(3\cdot5-8\cdot1) \\ &=\hat\imath(-50)-\hat\jmath(-17)+\hat k(7) =(-50,17,7) \end{aligned}\]

   lh 

8. Find \(\vec u\times\vec v+\vec u\times\vec w\) if \(\vec u=(3,2,1)\), \(\vec v=(3,-2,4)\) and \(\vec w=(-2,2,-4)\).

   Use the Distributive Rule first, (i.e. factor).

   \(\vec u\times\vec v+\vec u\times\vec w=\langle0,1,-2\rangle\)

   We first simplify by factoring the expression: \[\begin{aligned} \vec u\times&\vec v+\vec u\times\vec w =\vec u\times(\vec v+\vec w) \\ &=\langle3,2,1\rangle\times\langle1,0,0\rangle =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 3 & 2 & 1 \\ 1 & 0 & 0 \end{vmatrix} \\ &=\hat\imath(0)-\hat\jmath(0-1) +\hat k(0-2) =\langle0,1,-2\rangle \end{aligned}\]

   py 

9. Let \(\vec u=(3,4,1)\), \(\vec v=(2,-2,2)\), and \(\vec w=(-1,3,0)\).

   1. Find \(\vec u\cdot\vec v\times\vec w\).

      To compute the triple product, calculate the determinant of the matrix containing the three vectors as rows: \[\begin{aligned} \vec u\cdot\vec v\times\vec w =\begin{vmatrix} w_1 & w_2 & w_3 \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} \end{aligned}\]

      \(\vec u\cdot\vec v\times\vec w=-22\)

      We expand on the third row because there is a \(0\): \[\begin{aligned} \vec u\cdot\vec v\times\vec w &=\begin{vmatrix} 3 & 4 & 1 \\ 2 & -2 & 2 \\ -1 & 3 & 0 \end{vmatrix} \\ &=-1[4\cdot2-1\cdot(-2)]-3[3\cdot2-1\cdot2]+0[*] \\ &=-1(10)-3(4) =-22 \end{aligned}\]

      lh 

   2. Find \(\vec w\times\vec v\cdot\vec u\).

      Think about the properties of the dot product and the cross product.

      \(\vec w\times\vec v\cdot\vec u=22\)

      Since the dot product is commutative while the cross product is anti-commutative: \[\begin{aligned} \vec w\times\vec v\cdot\vec u &=\vec u\cdot\vec w\times\vec v \\ &=-\vec u\cdot\vec v\times\vec w =22 \end{aligned}\] from part (a).

      lh,py 

10. Find the triple product \(\vec u\cdot\vec u\times\vec v\) if \(\vec u=(1,3,2)\) and \(\vec v=(2,4,3)\)

    Think about the properties of the triple product. What happens if \(2\) vectors are equal?
    Equivalently, recall the cross product \(\vec u\times\vec v\) is perpendicular to both \(\vec u\) and \(\vec v\).

    \(\vec u\cdot\vec u\times\vec v=0\)

    When \(2\) vectors are equal, the triple product is \(0\): \[ \vec u\cdot\vec u\times\vec v=0 \] Equivalently, \(\vec u\times\vec v\) is perpendicular to \(\vec u\): \[ \vec u\cdot\vec u\times\vec v=0 \] We can also just compute the triple product by expanding on the third row: \[\begin{aligned} \vec u\cdot\vec u\times\vec v &=\begin{vmatrix} 1 & 3 & 2 \\ 1 & 3 & 2 \\ 2 & 4 & 3 \end{vmatrix} \\ &=2(6-6)-4(2-2)+3(3-3) \\ &=0 \end{aligned}\]

    lh,py 

11. Find the magnitude of the cross product, \(|\vec u\times\vec v|\), if \(\vec u=\left\langle -1,6,3\right\rangle\) and \(\vec v=\left\langle 2,2,1\right\rangle\)

    \(|\vec u\times\vec v| =7\sqrt{5}\approx 15.65\)

    We compute the cross product: \[\begin{aligned} \vec u\times\vec v &=\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ -1 & 6 & 3 \\ 2 & 2 & 1 \end{vmatrix} \\ &=\hat\imath(6\cdot1-3\cdot2)-\hat\jmath(-1\cdot1-3\cdot2) \\ &\quad+\hat k(-1\cdot2-6\cdot 2) \\ &= \hat\imath(0)-\hat\jmath(-7)+\hat k(-14)| \\ &= \langle 0,7,-14 \rangle \end{aligned}\] and then find its magnitude: \[ |\vec u\times\vec v| =\sqrt{7^2+14^2} =7\sqrt{5}\approx 15.65 \]

    lh,py 

c. Area

1

12. Find the area of the parallelogram with adjacent edges \(\vec u=(1,3,4)\) and \(\vec v=(1,2,5)\).

    

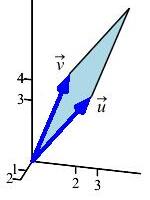
    Use the formula for area of a parallelogram given adjacent edges: \[\begin{aligned} A_{\textstyle\diamond}=|\vec u\times\vec v| \end{aligned}\]

    \(A_{\textstyle\diamond}=|\vec u\times\vec v|=\sqrt{51}\approx 7.14\)

    The area of the parallelogram is: \[\begin{aligned} A_{\textstyle\diamond} &=|\vec u\times\vec v| =\left|\rule{0pt}{25pt} \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 1 & 3 & 4 \\ 1 & 2 & 5 \end{vmatrix} \right| \\ &=|\hat\imath(15-8)-\hat\jmath(5-4)+\hat k(2-3)| \\ &=\left|\left\langle 7,-1,-1\right\rangle\right| \\ &=\sqrt{7^2+(-1)^2+(-1)^2}=\sqrt{51}\approx 7.14 \end{aligned}\]

    lh 

13. Find the area of the triangle with adjacent edges \(\vec a=(2,-1,4)\) and \(\vec b=(-1,2,0)\).

    

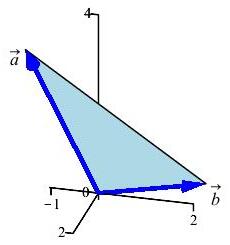
    Use the formula for area of a triangle given adjacent edges: \[ A_\triangle =\dfrac{1}{2}|\vec u\times\vec v| \]

    \(A_\triangle=\dfrac{1}{2}|\vec a\times\vec b| =\dfrac{1}{2}\sqrt{89}\approx 4.72\)

    The area of the triangle is: \[\begin{aligned} A_\triangle&=\dfrac{1}{2}|\vec a\times\vec b| =\dfrac{1}{2}\left|\rule{0pt}{25pt} \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2 & -1 & 4 \\ -1 & 2 & 0 \end{vmatrix} \right| \\ &=\dfrac{1}{2}[\hat\imath(0-8)-\hat\jmath(0+4)+\hat k(4-1)] \\ &=\dfrac{1}{2}|\left\langle -8,-4,3\right\rangle| =\dfrac{1}{2}\sqrt{64+16+9} \\ &=\dfrac{1}{2}\sqrt{89} \approx 4.72 \end{aligned}\]

    lh 

14. Find the area of a parallelogram with adjacent edge vectors \(\vec p\) and \(\vec q\), if \(|\vec p|=2\), \(|\vec q|=3\), and the angle between them is \(\theta=30^\circ\).

    

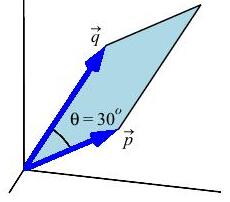
    Use the geometric definition of the cross product to help solve this problem: \[\begin{aligned} \vec p\times\vec q=|\vec p|\,|\vec q|\sin\theta \end{aligned}\]

    \(A_{\textstyle\diamond}=|\vec p\times\vec q|=3\)

    The area of the parallelogram is: \[\begin{aligned} A_{\textstyle\diamond}&=|\vec p\times\vec q| =|\vec p|\,|\vec q|\sin\theta \\ &=2\cdot3\cdot\sin30^\circ =6\cdot\dfrac{1}{2}=3 \end{aligned}\]

    lh 

15. Find the area of the triangle with adjacent edge vectors \(\vec u\) and \(\vec v\), if \(|\vec u|=5\), \(|\vec v|=2\), and the angle between them is \(\theta=45^\circ\).

    

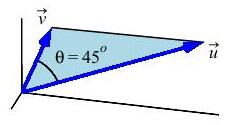
    \(A_\triangle=\dfrac{5\sqrt{2}}{2}\)

    The area of the triangle is: \[\begin{aligned} A_\triangle&=\dfrac{1}{2}(\vec u\times\vec v) =\dfrac{1}{2}|\vec v|\,|\vec u|\sin\theta \\ &=\dfrac{1}{2}(5\cdot2)\sin45^\circ =\dfrac{5\sqrt{2}}{2} \end{aligned}\]

    lh 

16. A triangle has vertices \(P=(2,3,4)\), \(Q=(4,3,2)\) and \(R=(5,0,4)\). Find its area.

    

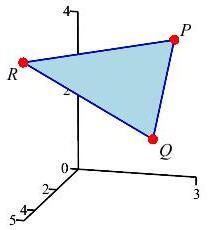
    The edge vectors are \(\overrightarrow{PQ}\) and \(\overrightarrow{PR}\).

    \(\displaystyle A_\triangle =\dfrac{1}{2}\left|\overrightarrow{PQ}\times\overrightarrow{PR}\right| =3\sqrt{3}\)

    The edge vectors are: \[ \overrightarrow{PQ}=Q-P=\langle2,0,-2\rangle \] and \[ \overrightarrow{PR}=R-P=\langle3,-3,0\rangle \] So the area of the triangle is: \[\begin{aligned} A_\triangle &=\dfrac{1}{2}\left|\overrightarrow{PQ}\times\overrightarrow{PR}\right| =\dfrac{1}{2}\left|\rule{0pt}{25pt} \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2 & 0 & -2 \\ 3 & -3 & 0 \end{vmatrix} \right| \\ &=\dfrac{1}{2}|\hat\imath(-6)-\hat\jmath(6)+\hat k(-6)| \\ &=\dfrac{1}{2}\left|\left\langle-6,-6,-6\right\rangle\right| \\ &=\dfrac{1}{2}\sqrt{36+36+36}=3\sqrt{3} \end{aligned}\]

    py 

17. A parallelogram has vertices \(A=(1,1,1)\), \(B=(1,2,3)\), \(C=(3,3,3)\) and \(D=(3,2,1)\), traversed in that order. Find its area.

    

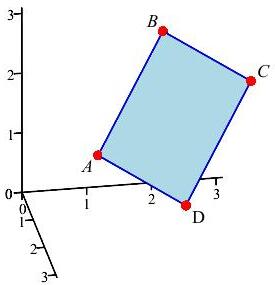
    The adjacent edge vectors are \(\overrightarrow{AB}\) and \(\overrightarrow{AD}\).

    \(\displaystyle A_{\textstyle\diamond}=\left|\overrightarrow{AB}\times\overrightarrow{AD}\right| =2\sqrt{6} \)

    The adjacent edge vectors are: \[ \overrightarrow{AB}=B-A=\langle0,1,2\rangle \] and \[ \overrightarrow{AD}=D-A=\langle2,1,0\rangle \]

    We check the other \(2\) edges are the same: \[\begin{aligned} \overrightarrow{DC}&=C-D=\langle0,1,2\rangle \\ \overrightarrow{BC}&=C-B=\langle2,1,0\rangle \end{aligned}\]

    So the area of the parallelogram is: \[\begin{aligned} A_{\textstyle\diamond}&=\left|\overrightarrow{AB}\times\overrightarrow{AD}\right| =\left|\rule{0pt}{25pt} \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 0 & 1 & 2 \\ 2 & 1 & 0 \end{vmatrix} \right| \\ &=|\hat\imath(-2)-\hat\jmath(-4)+\hat k(-2)| \\ &=\left|\left\langle -2,4,-2\right\rangle\right| \\ &=\sqrt{4+16+4}=\sqrt{24}=2\sqrt{6} \end{aligned}\]

    py 

18. If \(\vec u=(0,2,2)\), \(\vec v=(0,0,2)\), then the angle between them is \(\theta=45^\circ\).

    

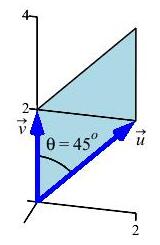
    1. Find the area of the parallelogram made by these vectors.

       \(A_{\textstyle\diamond}=4\)

       The area of the parallelogram is: \[\begin{aligned} A_{\textstyle\diamond} &=|\vec u\times\vec v| =|\vec u|\,|\vec v|\sin\theta \\ &=\sqrt{8}\cdot\sqrt{4}\sin45^\circ =4 \end{aligned}\]

       lh 

    2. Find the area of each triangle made by these vectors.

       \(A_\triangle=2\)

       The area of the triangle is half that of the parallelogram: \[ A_\triangle=2 \]

       lh 

       Since the triangle is an isoceles right triangle with sides \(s=2\), its area is just \(A_\triangle=\dfrac{1}{2}s^2=2\) and the area of the parallelogram is \(A_{\textstyle\diamond}=2A_\triangle=4\).

d. Volume

1

2

19. Find the volume of the parallelpiped with adjacent edge vectors \(\vec u=(1,3,5)\), \(\vec v=(2,5,6)\), and \(\vec w=(9,6,3)\).

    

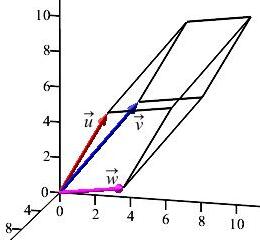
    The volume of the parallelpiped is the absolute value of the triple product of the three adjacent edge.

    \(V=42\)

    The volume of the parallelpiped is: \[\begin{aligned} V&=|\vec u\cdot \vec v\times \vec w| =\left|\rule{0pt}{25pt} \begin{vmatrix} 1 & 3 & 5 \\ 2 & 5 & 6 \\ 9 & 6 & 3 \end{vmatrix}\right| \\ &=|1(15-36)-3(6-54)+5(12-45)| \\ &=|-21+144-165| =|-42|=42 \end{aligned}\]

    lh 

20. Find the volume of the parallelpiped with adjacent edges \(\vec a=\left\langle4,2,1\right\rangle\), \(\vec b=\left\langle3,0,-1\right\rangle\), and \(\vec c=\left\langle1,1,1\right\rangle\)

    

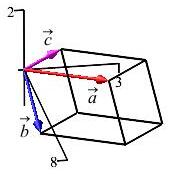
    \(V=1\)

    The volume of the parallelpiped is: \[\begin{aligned} V&=|\vec a\cdot \vec b\times \vec c| =\left|\rule{0pt}{25pt} \begin{vmatrix} 4 & 2 & 1 \\ 3 & 0 & -1 \\ 1 & 1 & 1 \end{vmatrix}\right| \\ &=|4(0-(-1))-2(3-(-1))+1(3-0)| \\ &=|4-8+3| =|-1|=1 \end{aligned}\]

    lh 

21. Find the volume of the parallelpiped with adjacent edges \(\overrightarrow{AB}\), \(\overrightarrow{AC}\), and \(\overrightarrow{AD}\) where \(A=(1,2,1)\), \(B=(2,3,2)\), \(C=(0,4,1)\), and \(D=(3,3,4)\).

    

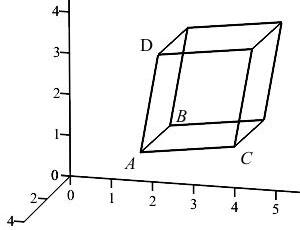
    First, determine the vectors \(\overrightarrow{AB}\), \(\overrightarrow{AC}\), and \(\overrightarrow{AD}\). Then use the triple product of the three vectors to find the volume of the parallelpiped.

    \(V=4\)

    The adjacent edges are: \[\begin{aligned} \overrightarrow{AB}&=\left\langle 2-1,3-2,2-1 \right\rangle =\left\langle 1,1,1 \right\rangle \\ \overrightarrow{AC}&=\left\langle 0-1,4-2,1-1 \right\rangle =\left\langle -1,2,0 \right\rangle \\ \overrightarrow{AD}&=\left\langle 3-1,3-2,4-1 \right\rangle =\left\langle 2,1,3 \right\rangle \end{aligned}\] So the volume is: \[\begin{aligned} V&=|\overrightarrow{AB}\cdot \overrightarrow{AC}\times \overrightarrow{AD}| =\left|\rule{0pt}{25pt} \begin{vmatrix} 1 & 1 & 1 \\ -1 & 2 & 0 \\ 2 & 1 & 3 \end{vmatrix}\right| \\ &=|1(6-0)-1(-3-0)+1(-1-4)| \\ &=|6+3-5| =|4|=4 \end{aligned}\]

    lh 

e. Applications

1

22. A rigid object is held fixed at the point \(P=(1,1,1)\).

    

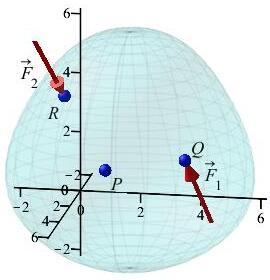
    1. Find the torque on the object, if the force \(\vec F_1=\langle1,-1,3\rangle\) is applied at the point \(Q=(3,4,2)\).

       First find the lever arm.

       \(\tau_1=\langle10,-5,-5\rangle\)

       The lever arm is: \[ \vec r_1=\overrightarrow{PQ}=Q-P=\langle2,3,1\rangle \] So the torque is: \[\begin{aligned} \tau_1&=\vec r_1\times\vec F_1 =\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2 & 3 & 1 \\ 1 & -1 & 3 \end{vmatrix} \\ &=\hat\imath(9+1)-\hat\jmath(6-1)+\hat k(-2-3) \\ &=\langle10,-5,-5\rangle \end{aligned}\]

       py 

    2. Find the torque on the object, if the force \(\vec F_2=\langle-4,2,-6\rangle\) is applied at the point \(R=(3,0,4)\).

       \(\tau_2=\langle0,0,0\rangle=\vec 0\)

       The lever arm is: \[ \vec r_2=\overrightarrow{PR}=R-P=\langle2,-1,3\rangle \] So the torque is: \[\begin{aligned} \tau_2&=\vec r_2\times\vec F_2 =\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2 & -1 & 3 \\ -4 & 2 & -6 \end{vmatrix} \\ &=\hat\imath(6-6)-\hat\jmath(-12+12)+\hat k(4-4) \\ &=\langle0,0,0\rangle=\vec 0 \end{aligned}\]

       py 

       The answer is obvious, if you notice that the force vector, \[ \vec F_2=\langle-4,2,-6\rangle=-2\langle2,-1,3\rangle \] is parallel to the lever are, \(\overrightarrow{PQ}=\langle2,-1,3\rangle\). Then their cross product is automatically zero.

23. A triangular plate with vertices \(P=(0,-1,0)\), \(Q=(0,1,0)\) and \(R=(2,0,0)\) is held fixed at the origin \(O=(0,0,0)\). The force \(\vec F_1=\left\langle 2,-1,0 \right\rangle\) is applied at \(P\) and the force \(\vec F_2=\left\langle -3,-1,0\right\rangle\) is applied at \(Q\). What force \(\vec F_3=\left\langle a,b,c\right\rangle\) can be applied at \(R\) to keep the triangle from rotating?

    

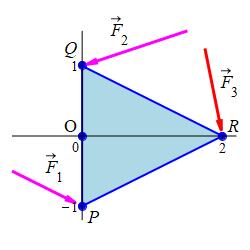
    In order for the triangle to remain motionless, the third torque must balance the other two, \(\vec\tau_3=-\vec\tau_1-\vec\tau_2\).
    
    To calculate the torques, first find the lever arms.

    \(\vec F_3=\left\langle a,-\,\dfrac{5}{2},0 \right\rangle\) for any \(a\).

    The lever arms and torques are: \[\begin{aligned} &\vec r_1=P-O=\left\langle 0,-1,0\right\rangle &\quad &\vec\tau_1=\vec r_1\times\vec F_1 =\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 0 & -1 & 0 \\ 2 & -1 & 0 \end{vmatrix} =\left\langle 0,0,2\right\rangle \\ &\vec r_2=Q-O=\left\langle 0,1,0\right\rangle &\quad &\vec\tau_2=\vec r_2\times\vec F_2 =\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 0 & 1 & 0 \\ -3 & -1 & 0 \end{vmatrix} =\left\langle 0,0,3\right\rangle \\ &\vec r_3=R-O=\left\langle 2,0,0\right\rangle &\quad &\vec\tau_3=\vec r_3\times\vec F_3 =\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2 & 0 & 0 \\ a & b & c \end{vmatrix} =\left\langle 0,-2c,2b\right\rangle \end{aligned}\] To balance the torques, we need \(\vec\tau_3=-\vec\tau_1-\vec\tau_2\). Or: \[ \left\langle 0,-2c,2b\right\rangle =-\left\langle 0,0,2\right\rangle-\left\langle 0,0,3\right\rangle =\left\langle 0,0,-5\right\rangle \] Consequently: \(c=0\), \(b=-\,\dfrac{5}{2}\) and \(\vec a\) is abitrary. So the torque is balanced by a force of the form, \(\vec F_3=\left\langle a,-\,\dfrac{5}{2},0\right\rangle\), for any \(a\).

    lh 

PY: All Checked

Review Exercises